Sampling Procedures

Conducting Educational Research
Step 6: Select Sampling Technique

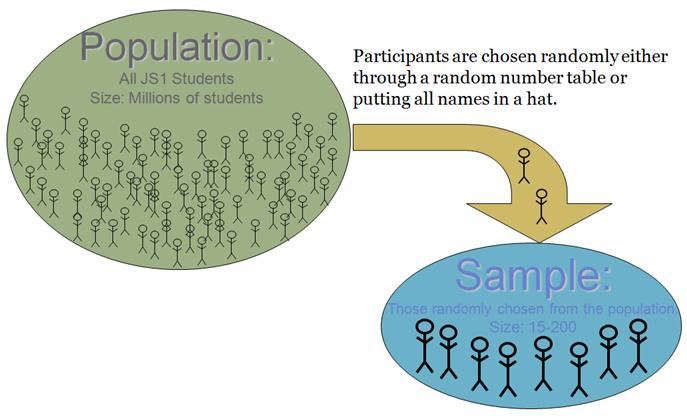
It is virtually impossible to study every individual in the target population. In most cases, the target population, such as students in JS1, is simply too large for the researcher to plan a quality research study. Collecting millions of questionnaires from every JS1 student would present the following challenges:

Millions of naira would be spent just to print the questionnaires, let alone transportation costs to distribute the questionnaires to all JS1 students.
Researchers would have difficulties finding all JS1 students, particularly in village areas.
Unqualified research assistants would have to be enlisted to assist in data collection, reducing the quality of data received.
Years would be spent distributing and collecting the questionnaires, let alone coding the questionnaire responses.
Since it will take so long to collect data from the entire population, the data from the first group of students sampled will likely be outdated by the time the last group of students is sampled.

Does this therefore mean that the target population has to be restricted to such a small group - such as all JS1 students in Baptist Academy - so that the researcher can access the entire population? NO! "Paradoxically, the attempt to observe all cases [in a population] may actually describe a population less accurately than a carefully selected sample...The reason is that the planning and logistics of observation are more manageable with a sample" (Singleton & Straits, 2010, p. 151). Research methodologists have developed sampling procedures that should identify a sample that is representative of the population, meaning that the sample closely resembles the target population on all relevant characteristics.

Theory of Sampling

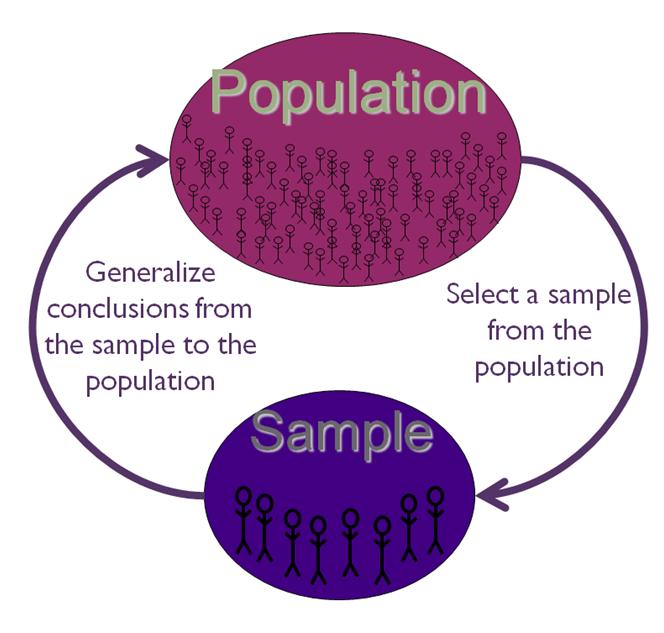
The theory of sampling is as follows:

Researchers want to gather information about a whole group of people (the population).
Researchers can only observe a part of the population (the sample).
The findings from the sample are generalized, or extended, back to the population.

Therefore, the key question in sampling is How representative is the sample of the target population? This question is the foundation of population validity, the degree to which the results of a study can be generalized from the sample to the target population.

The analogy of a fruit market can be used when thinking about the population, the sample, and the sampling technique. The first step in sampling is to identify the unit of analysis. This was described in Chapter 11, Identify the Population. Let's say that you are conducting research related to a fruit market. What will be studied in the fruit market? Is it a type of fruit or the fruit sellers themselves? Let's say you identify citrus fruit as the unit of analysis, and your population is all citrus fruit within the Bauchi Road fruit market. There are too many pieces of citrus fruit for you to study in that market, so you must select only a sample of the citrus fruit.

A common error in sampling is that the sample and population are not identical. For example, the sample may be too narrow. If the population is all citrus fruit within the Bauchi Road fruit market, then the sample cannot only consist of lemons because your sample would be missing oranges, grapefruit, and limes. Therefore, you must find a way of selecting a representative sample of citrus fruit from your population. To apply to an educational study, perhaps one may say that the population is all university students, but only university students in public schools are sampled.

Another common error is to make the population too broad. Some may say that the population is all mangoes in the Bauchi Road fruit market, but they are really only interested in green mangoes. If only green mangoes are of interest, then the population should be green mangoes in the Bauchi Road fruit market. In educational research, sometimes researchers are only interested in a population with a certain characteristic, such as student who has not chosen a career (in the case of career counseling). Thus, the population and sample must be the same.

Preliminary Considerations in Selecting a Sample

Before selecting a sampling procedure, first consider the following:

Select the unit of analysis. When selecting the sample, it is imperative that the sampling technique selects cases based on this unit of analysis. In other words, if the unit of analysis is students, then the sampling technique must focus solely on how the students were selected. It would be an error to describe the selection of schools as the sampling technique when the unit of analysis is students.
Determine how many units need to be sampled. This step is a tricky balancing act. On the one hand, larger samples tend to be more representative of the target population and provide stronger statistical power. On the other hand, larger samples can decrease the quality of the research study, particularly for experimental and quasi-experimental designs. In experimental designs, if many people participate in the treatment, then the quality of treatment that each individual receives might suffer, resulting in inaccurate conclusions. It is a truism that overpopulation in classrooms reduces the impact of instruction; if there are too many students in the class, then the teaching will not be as effective. Likewise, we should equally avoid the problem of overpopulation in experiments: too many participants in a treatment group will reduce the impact of the treatment. Therefore, smaller treatment groups are generally preferable. In general, descriptive designs require at least 100 participants, correlational designs require at least 30 participants, and experimental, quasi-experimental, and causal-comparative designs require at least 15 participants per group. The size of the sample in experiments depend on how effective the treatment is. If you have a very effective treatment, then only a few participants are necessary. However, if the treatment is weak, then a larger sample size is necessary to find a significant effect.

Sampling Procedures

There are many sampling procedures that have been developed to ensure that a sample adequately represents the target population. A few of the most common are described below.

Simple Random Sampling
In simple random sampling, every individual in the target population has an equal chance of being part of the sample. This requires two steps:

Obtain a complete list of the population.
Randomly select individuals from that list for the sample.

Recall that the sampling procedure must reflect the unit of analysis. In a study where the unit of analysis is the student, the researcher must obtain a complete list of every student in the target population to achieve simple random sampling. This is rarely possible, so very few, if any, educational studies use simple random sampling.

Another factor to consider is the word random. Random is a technical term in social science research that means that selection was made without aim, reason, or patterns. If any study uses the word random, it means that specific scientific procedures were used to ensure that the sample was selected purely by chance. Scientists have developed a few procedures that must be followed for a study to achieve random, such as the hat-and-draw method or a random number table. To be random, participants cannot be chosen because of their intelligence, gender, social class, convenience, or any other factor besides scientifically-agreed upon random procedures. Using the word random when the unit of analysis was not selected by the hat-and-draw method or a random number table is either irresponsible or flat-out untruthful.

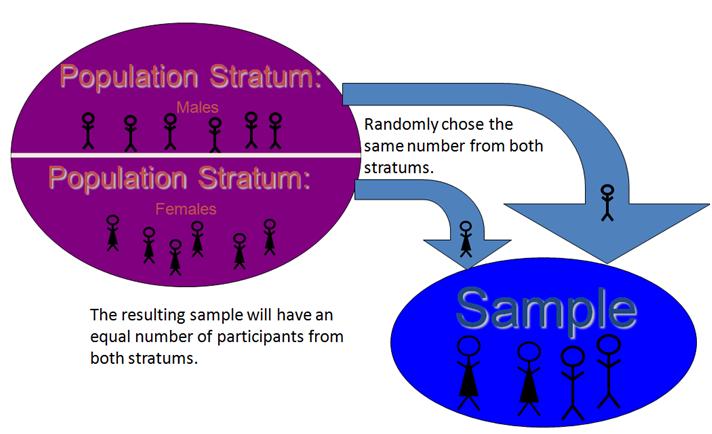
Stratified Random Sampling
In stratified random sampling, the researcher first divides the population into groups based on a relevant characteristic and then selects participants within those groups. In educational research, stratified random sampling is typically used when the researcher wants to ensure that specific subgroups of people are adequately represented within the sample. For example, a research study examining the effect of computerized instruction on maths achievement needs to adequately sample both male and female pupils. Stratified random sampling will be used to ensure adequate representation of both males and females. Stratified random sampling requires four steps:

Determine the strata that the population will be divided into. The strata are the characteristics that the population is divided into, perhaps gender, age, urban/rural, etc.
Determine the number of participants necessary for each stratum. Perhaps the researcher wants equal representation within the strata: half male, half female; 20 children age 5, 20 children age 6, and 20 age 7; etc. Other times (e.g., large survey research), the researcher might want to use proportionate random sampling. This requires that the researcher first knows the proportion of the group in the entire population and then match that proportion within the sample. For example, a researcher might find the most recent Nigerian census to determine that females represent 53% of the population in Nigeria, so the sample will then include 53% females.
Split the units of analysis into the respective strata. In other words, if the target population is students and the researcher wants to stratify based on gender, then the researcher will need two lists of the target population: one list of the male students and another list of the female students.
Randomly sample participants from within the group. Using either the hat-and-draw method or a random number table, randomly select the requisite number of males and do the same for the females.

Purposive Sampling
In purposive sampling, the researcher uses their expert judgment to select participants that are representative of the population. To do this, the researcher should consider factors that might influence the population: perhaps socio-economic status, intelligence, access to education, etc. Then the researcher purposefully selects a sample that adequately represents the target population on these variables.

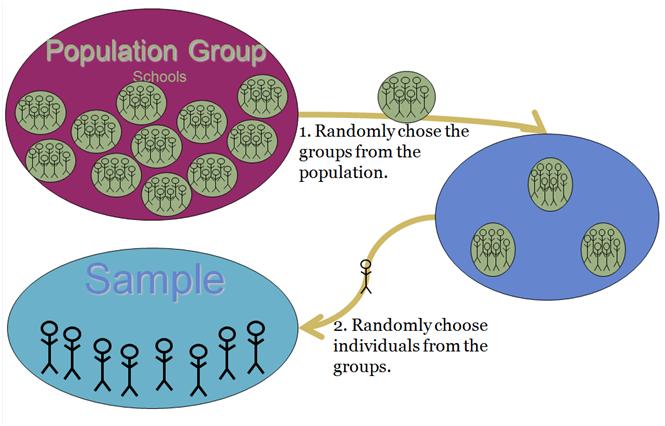
Multi-Stage Sampling
More frequently, educational researchers use multi-stage sampling. In multi-stage sampling, the sample is selected in multiple steps, or stages. For example, in the first stage, geographical regions, such as local government areas, are selected. In the second stage, perhaps schools may be selected. In the third stage, the unit of analysis - perhaps teachers or students, are sampled. If the unit of analysis is not selected in the first step, then the sampling procedure is multi-stage sampling. In multi-stage sampling, other sampling techniques may be used at the different stages. For example, the first stage may use random sampling, the second stage may use purposive sampling, and the third stage may use stratified sampling.

The steps in multi-stage sampling are as follows:

Organize the sampling process into stages where the unit of analysis is systematically grouped.
Select a sampling technique for each stage.
Systematically apply the sampling technique to each stage until the unit of analysis has been selected.

Conclusion

Recall that the key question in sampling is How representative is the sample of the target population? Therefore, the researcher has the burden of demonstrating in their report (primarily in the methods section) that their sample, regardless of how it was chosen, represents the target population. Simple random sampling or multi-stage sampling will typically answer this question the best. However, as long as the researcher makes a convincing argument in their methods section that their sample adequately represents the target population, the researcher really can use any available sampling procedure.

Return to Educational Research Steps